<< Назад  |   Оглавление  |   Далее >>

4.8. Прямоугольник и его площадь

Прямоугольник

Прямоугольником называется параллелограмм [4.4], в котором один из углов — прямой, то есть равен четверти оборота (90°).

 

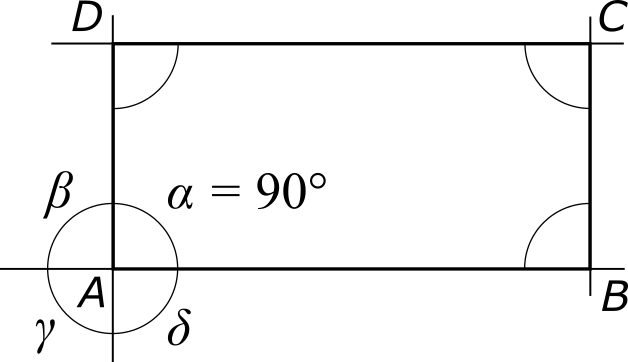
Рассмотрим прямоугольник ABCD с прямым углом α при вершине A. Докажем, что все остальные углы прямоугольника тоже равны 90°. Продолжим стороны прямоугольника до прямых. Поскольку один из углов, образованных при пересечении прямых AB и AD (а именно α), равен 90°, то и остальные углы (а именно β, γ и δ) тоже равны 90° [4.2]. Угол при вершине B является соответственным углу β (при параллельных прямых), а угол при вершине D — соответственным углу δ, и потому они также равны 90°. Что же касается угла при вершине C, то мы уже знаем, что противоположные углы в параллелограмме равны между собой [4.4]. На этом доказательство закончено.

Длина любой из сторон прямоугольника может быть названа длиной прямоугольника, а также его шириной или высотой. При этом длину соседней стороны называют каким-либо другим словом из этого же набора.

Построение прямого угла

Чтобы чертить прямоугольники, надо уметь строить прямые углы. Это можно, в принципе, делать с помощью транспортира, однако гораздо удобнее воспользоваться школьным угольником, у которого один из углов всегда делается прямым.

Задача 4.8.1a. Провести две произвольные перпендикулярные прямые.

 

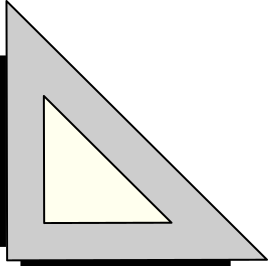
Берем угольник и проводим прямые линии вдоль его коротких сторон. При необходимости потом можно с помощью линейки продолжить линии таким образом, чтобы они пересеклись.

Задача 4.8.1b. Провести через заданную точку прямую, перпендикулярную к заданной прямой. Или, как еще говорят в таких случаях: опустить из точки перпендикуляр на прямую. Предполагается, что точка не лежит на прямой.

 

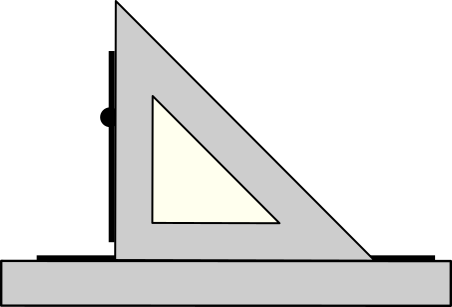
Совмещаем одну из сторон линейки с заданной прямой. Прикладываем угольник короткой стороной к линейке. Скользим угольником вдоль линейки до тех пор, пока другая его короткая сторона не окажется возле заданной точки. Проводим через точку прямую линию по угольнику. При необходимости с помощью линейки продолжаем новую линию до ее пересечения со старой.

Задача 4.8.1с. Дана прямая и точка на ней. Провести через эту точку перпендикуляр.

 

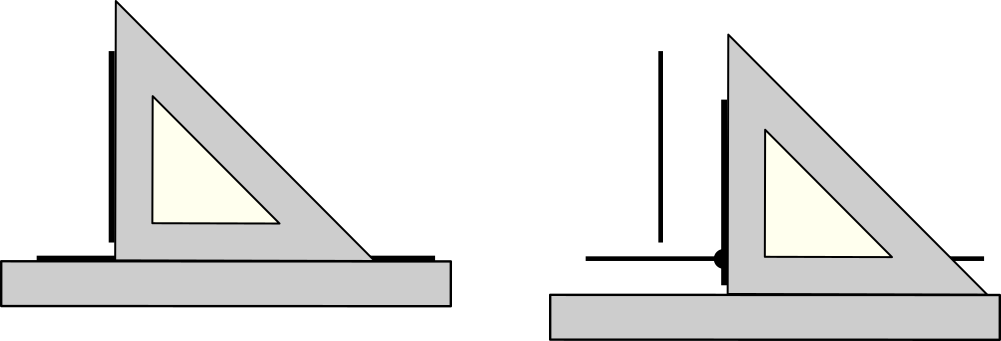
При известной сноровке и хорошем глазомере, эту задачу можно решить тем же способом, что и предыдущую. Но есть и более верное решение. Строим произвольный перпендикуляр к данной прямой и проводим параллельную ему прямую через заданную точку.

Площадь прямоугольника

Задача 4.8.2. Полоса бумаги

шириной a₀ = 2 см и длиной b₀ = 50 см

весит m₀ = 0,8 г. Сколько весит лист той же бумаги

высотой a = 30 см и шириной b = 20 см?

Иными словами, нам известна масса m₀ такого прямоугольника, вырезанного из бумаги:

 

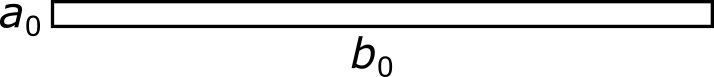
А требуется найти массу m такого прямоугольника:

 

Расположим оба прямоугольника на одной плоскости, как показано на рисунке, и добавим еще один, вспомогательный, прямоугольник, изготовленный всё из той же бумаги:

 

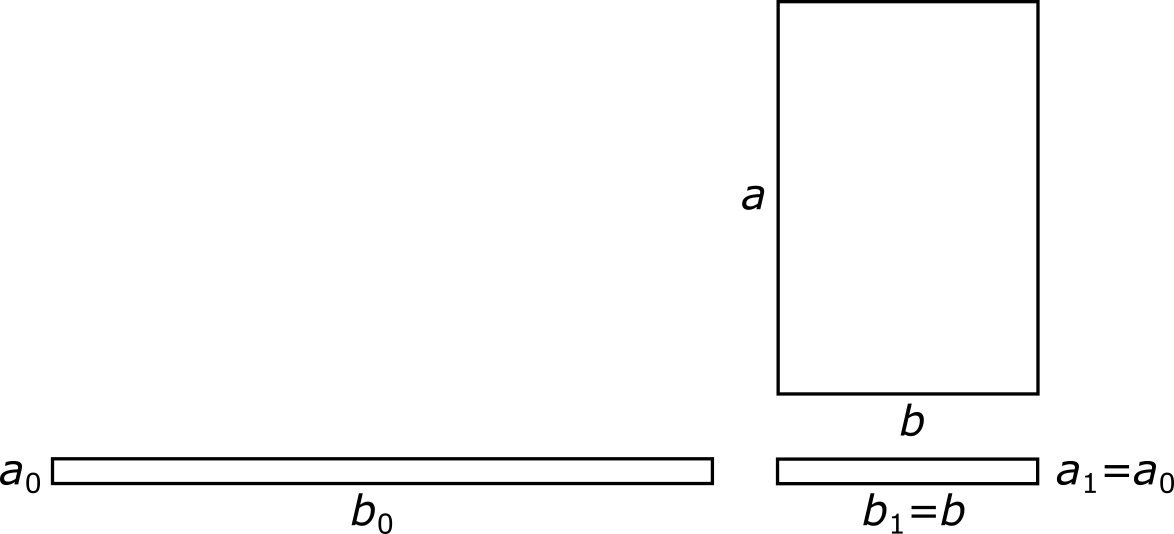
Вспомогательный прямоугольник нарочно сделан так, чтобы его вертикальный размер a₁ был точно таким же, как и у прямоугольника-полосы с известной массой: a₁ = a₀, а горизонтальный размер b₁ — точно таким же, как и у прямоугольника-листа с неизвестной массой: b₁ = b. Умея решать задачи на пропорции, мы теперь можем по массе прямоугольника-полосы найти массу вспомогательного прямоугольника. А зная массу вспомогательного прямоугольника, мы можем найти массу прямоугольника-листа. Для этого составим такую табличку:

 

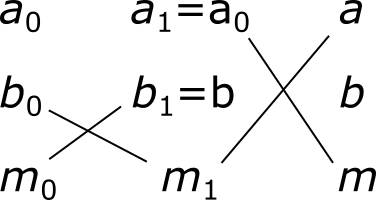
Отсюда

m1 =	m0	∙ b1 =	0,8 г	∙ 20 см = 0,32 г.
	b0		50 см

m =	m1	∙ a =	0,32 г	∙ 30 см = 4,8 г.
	a1		2 см

Для полноты картины выпишем решение  в общем виде (помня о том, что a₁ = a₀ и b₁ = b):

m = m1	a	=	m0	b1	a	=	m0	b1a =	m0	ab.
	a1		b0		a1		b0a1		a0b0

Мы получили формулу зависимости массы листа бумаги m от его размеров a и b. Эта формула верна при любых численных значениях a₀ и b₀. Покуда мы имеем дело с одним и тем же сортом бумаги, дробь m₀/a₀b₀ остается всё время равной одному и тому же числу (имеющему размерность г/см²). Это число называется поверхностной плотностью и (так же как и в случае линейной плотности) часто обозначается греческой буквой ρ:

ρ =	m0	=	m	.
	a0b0		ab

В условиях нашей задачи

ρ =	0,8 г	= 0,008	г	= 0,008	г	= 80	г	.
	2 см∙50 см		см2		(0,01м)2		м2

(Это — наиболее типичная поверхностная плотность бумаги, используемой в офисах для принтеров и копировальных аппаратов. Ее значение приводится на упаковках, в которых поставляется бумага.)

Произведение ab носит название площади прямоугольника со сторонами a и b. Площадь обычно обозначается буквой S:

S = ab.

Чтобы найти массу m листа бумаги, надо поверхностную плотность ρ бумаги умножить на площадь листа S. Иначе говоря, масса m пропорциональна площади S с коэффициентом пропорциональности ρ:

m = ρ∙S = ρ∙ab.

Конспект

1. Прямоугольник — это параллелограмм, у которого все углы прямые. При этом достаточно потребовать, чтобы хотя бы один угол был равен 90°. Равенство остальных углов 90° следует автоматически.

2. Площадь прямоугольника S — это произведение длин его соседних сторон a и b: S = ab. Одну из этих длин называют длиной, другую — шириной (возможны другие комбинации названий: длина и высота, ширина и высота).

3. Поверхностная плотность ρ листового материала, имеющего форму прямоугольника со сторонами a и b, может быть найдена как отношение его массы m к площади поверхности: ρ = m/S = m/ab. Наоборот, если известна поверхностная плотность, то масса прямоугольного листа рассчитывается по формуле m = ρ∙S = ρ∙ab.