<< Назад  |   Оглавление  |   Далее >>

4.4. Симметрия относительно точки. Параллелограмм

Немного терминологии

Пусть нам даны на плоскости две произвольные прямые m и n. Отметим на прямой m какую-либо точку M, а на прямой n — какую-либо точку N. Проведем третью прямую через точки M и N. При этом образуется две четверки углов, как показано на рисунке:

 

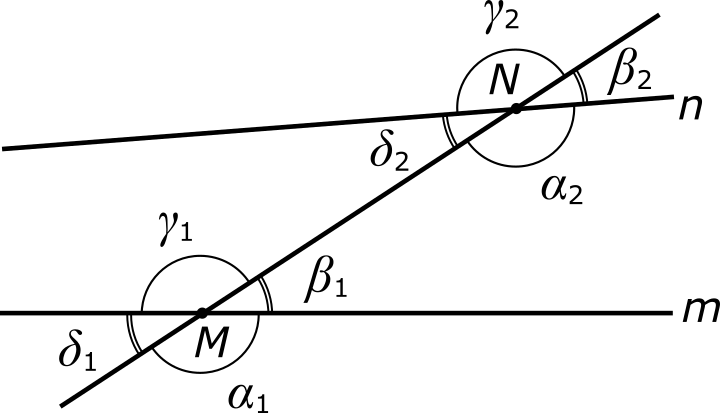
Здесь у дуг, обозначающих углы, отсутствуют стрелочки, поскольку нас сейчас интересуют угловые расстояния, а не угловые смещения. Можно сказать, что в данной геометрической конструкции угол α₁ соответствует углу α₂. Именно так эти углы и называются — соответственными по отношению друг к другу. Аналогичным образом, соответственными являются пары углов:

β₁ и β₂,
γ₁ и γ₂,
δ₁ и δ₂. 

(Замечу в скобках, что похожие по смыслу величины у математиков принято обозначать одинаковыми буквами и различать их по так называемому индексу — числовому или буквенному довеску, приписываемому справа внизу мелким шрифтом. Так, в обозначении α₁ основным символом является α, а индексом — число 1.)

На прошлом уроке мы ввели понятие параллельных прямых: две несовпадающие прямые называются параллельными, если угол между ними равен нулю.

 

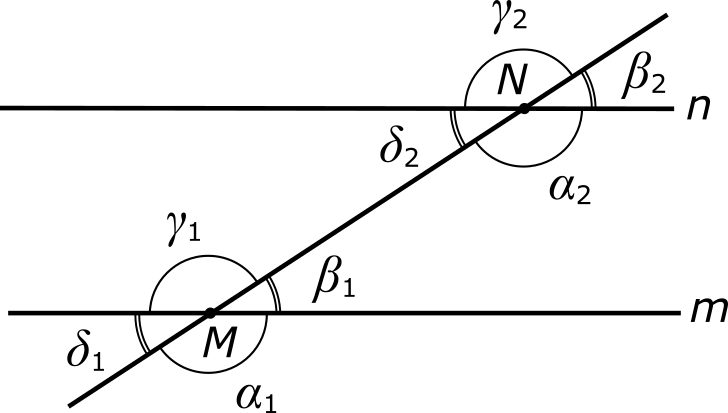
Угол же между двумя прямыми всегда можно найти как разность соответственных углов, образуемых при пересечении с какой-либо третьей прямой. Так, угол φ между прямыми m и n равен

φ = |α₂ − α₁|.

Здесь мы взяли результат по абсолютной величине, поскольку речь идет об угловом расстоянии, а не об угловом смещении. При этом совершенно безразлично, какую пару соответственных углов брать. С тем же успехом мы могли бы написать

φ = |β₂ − β₁|,
φ = |γ₂ − γ₁|,
φ = |δ₂ − δ₁|.

Действительно, угол β₁ является смежным с углом α₁, а угол β₂ — смежным с углом α₂, следовательно,

β₁ = 180° − α₁,
β₂ = 180° − α₂,
|β₂ − β₁| = |α₂ − α₁|.

По точно такой же причине,

|δ₂ − δ₁| = |α₂ − α₁|.

Что же касается углов γ₁ и γ₂, то они являются вертикальными по отношению к α₁ и α₂, а потому

γ₁ = α₁,
γ₂ = α₂,

Значит, угол φ между прямыми n и m можно найти как

φ = |α₂ − γ₁|.

Углы α₂ и γ₁ в рассматриваемой геометрической конструкции называются внутренними накрест лежащими. Другой парой внутренних накрест лежащих углов здесь являются углы δ₂ и β₁, разность которых также можно использовать для нахождения угла φ:

φ = |δ₂ − β₁|.

Таким образом, две прямые, пересеченные какой-либо третьей, являются параллельными тогда и только тогда, когда внутренние накрест лежащие углы равны между собой.

Симметрия относительно точки

Рассмотрим на плоскости две произвольные параллельные прямые m и n. Пусть M — какая-либо точка, принадлежащая прямой m, а N — какая-либо точка, принадлежащая прямой n. Соединим эти точки отрезком MN. Выберем какую-либо пару накрест лежащих углов и обозначим каждый из них буквой α (мы вправе это сделать, потому что эти углы равны между собой).

 

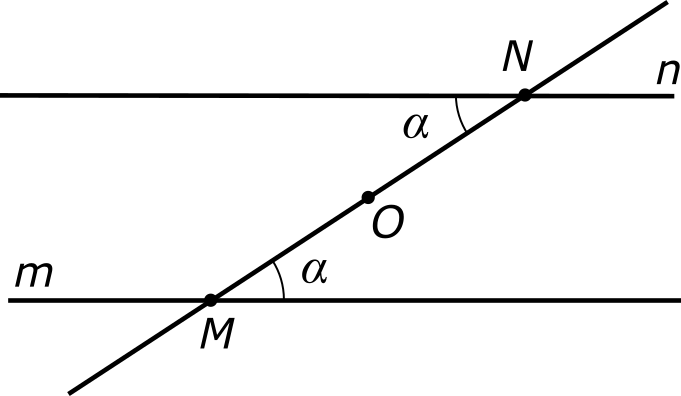
Отметим на отрезке MN середину и обозначим ее буквой O. В скором времени мы научимся изящному способу делить отрезок на любое число частей, но пока мы можем просто измерить длину отрезка MN (напомню, что она обозначается как |MN|), поделить ее пополам: |MN|/2, а потом отложить указанное расстояние вдоль отрезка MN, начиная от любого из его концов.

Теперь, не выходя из плоскости, повернем полученную геометрическую конструкцию на полоборота (180°) вокруг точки O. При этом, как это принято в математике, за старыми положениями точек M и N сохраняются старые обозначения, а для их новых положений мы должны подобрать новые обозначения, например, M₁ и N₁. Это же относится и к обозначениям прямых. Если до поворота они обозначались как m и n, то после поворота они должны обозначаться как-то по-другому, например, m₁ и n₁.

 

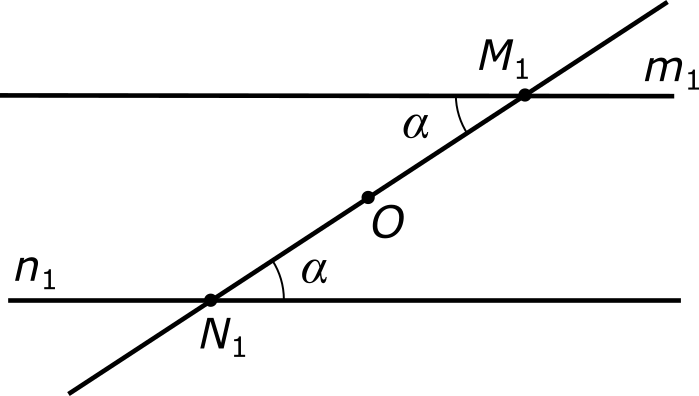
Примечание. Когда мы вводили понятие точки, мы отмечали, что, если не оговорено противное, точки считаются неподвижными. Теперь к этому необходимо добавить, что только неподвижные точки могут иметь собственные обозначения, такие как M, N, M₁, N₁ и т.п. Подвижная же точка собственного обозначения никогда не имеет и распознается по той неподвижной точке, где она в данный момент находится. Это же относится и, вообще, к любым подвижным геометрическим объектам (прямым, отрезкам и др.).

Нетрудно видеть, что местоположение точки N₁ полностью совпадает с местоположением точки М, то есть фактически это одна и та же точка. Подобным же образом, точка М₁ совпадает с точкой N. Более того, из-за равенства накрест лежащих углов прямая n₁ в точности ложится на прямую m, а прямая m₁ — на прямую n. Возвращаясь к первоначальным обозначениям, мы приходим к тому же самому положению вещей, которое было до поворота:

 

Мы рассмотрели частный случай так называемой симметрии относительно точки. В общем случае эта симметрия определяется следующим образом. Пусть на плоскости задана некоторая точка O. Симметрией относительно этой точки называется поворот вокруг нее на угол 180° (в пределах той же плоскости).

При этом сама точка O называется центром симметрии.

Точки М и N, переходящие друг в друга в результате такого поворота, называются симметричными (одна по отношению к другой). Центр симметрии O лежит на отрезке МN и делит его в точности пополам.

Также называются симметричными любые пары геометрических объектов (прямых, отрезков и т.п.), если они переходят друг в друга.

Про геометрическую конструкцию, которая переходит сама в себя, говорят, что она центрально-симметрична или же что она обладает центром симметрии (подразумевая под таким центром точку O).

Пусть даны две произвольные точки M и O. Чтобы построить точку N, симметричную точке M относительно центра O, надо проделать следующее.

 

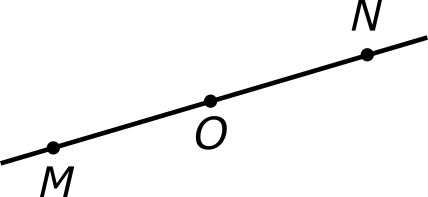
Проведем прямую OM. Направление от O к M примем за положительное. Отложим от точки O вдоль прямой в отрицательном направлении отрезок ON, равный по длине отрезку OM. Угол ∠MON равен по величине 180°, а значит, его стороны получаются друг из друга поворотом на 180° (безразлично в каком направлении), при этом точка M переходит в точку N, и наоборот, точка N переходит в точку M. Таким образом, эти точки являются симметричными.

Перечислим некоторые очевидные свойства симметрии относительно точки.

Прямая центрально-симметрична относительно любой из своих точек.

Отрезок центрально-симметричен относительно своей середины.

Если точки M и N симметричны, то центр симметрии O совпадает с серединой отрезка MN.

Параллельные прямые симметричны относительно середины отрезка, один из концов которого лежит на одной прямой, а другой конец — на другой прямой. (Мы это доказали чуть выше).

Параллелограмм

Вернемся к паре параллельных прямых m и n из предыдущего пункта. Отметим на прямой m произвольную точку K, не совпадающую с M, и проведем через точки K и N прямую, которую мы обозначим буквой k.

 

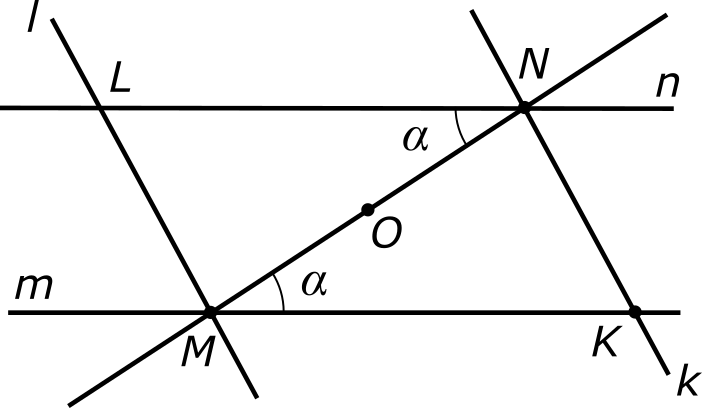
Далее, проведем через точку M еще одну прямую, параллельную k, и обозначим ее через l. Мы снова пришли к симметричной конструкции. Мы имеем:

Прямые m и n симметричны, как было показано ранее.

Прямые k и l симметричны по той же причине, что и прямые m и n.

Прямые k и m пересекаются в точке K.

Следовательно, у прямых l и n также есть точка пересечения, которая симметрична точке K. Обозначим ее буквой L.

У нас образовалась замкнутая цепочка из четырех отрезков LM, MK, KN и NL. В этой цепочки соседние отрезки имеют общие концы, а противоположные отрезки параллельны (то есть лежат на параллельных прямых). Внутренняя часть плоскости, ограниченная такой цепочкой, называется параллелограммом.

Отрезки, служащие границей, также принадлежат параллелограмму и называются его сторонами.

Концы сторон, где они соединяются друг с другом, называются вершинами параллелограмма.

Внутренние углы между соседними сторонами (при вершинах) называются углами параллелограмма.

Отрезки, соединяющие противоположные вершины параллелограмма, называются его диагоналями.

Всего у параллелограмма две диагонали, из которых мы пока построили только одну — отрезок MN. Проведем другую диагональ — KL. Она пересекает первую диагональ в точке O и делится этой точкой пополам (в силу симметричности конструкции).

 

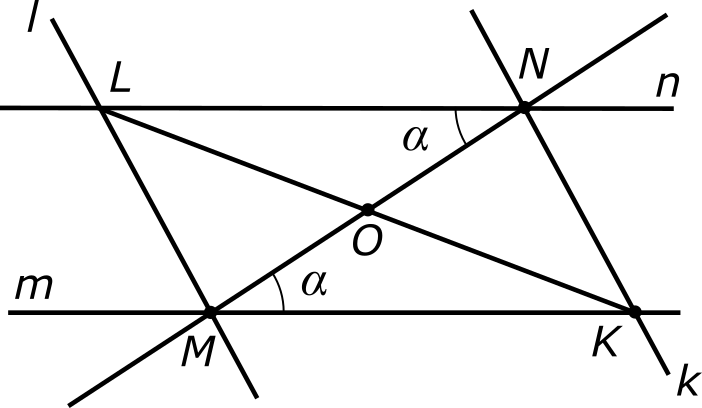
Таким образом, мы установили, что параллелограмм обладает центром симметрии, который находится в точке пересечения диагоналей. Вот еще два полезных свойства параллелограмма, следующие из его симметричности:

Длины противоположных сторон параллелограмма одинаковы.

Противоположные углы параллелограмма равны между собой.

Параллелограмм обычно обозначают, перечисляя его вершины. Параллелограмм, который мы построили в данном случае, можно обозначить как LMKN.

Конспект

Угол между двумя прямыми, пересеченными третьей прямой, может быть найден как разность соответственных углов или же как разность внутренних накрест лежащих углов. В обоих случаях разность следует брать по абсолютной величине.

Две прямые, пересеченные третьей, параллельны тогда и только тогда, когда соответственные углы равны между собой. Такое же утверждение справедливо и для внутренних накрест лежащих углов.

Симметрия относительно точки O: поворот вокруг этой точки на 180° (в пределах заданной плоскости).

Построение точки N, которая симметрична точке M относительно центра O: на прямой OM откладываем отрезок ON, равный по длине |OM|, в противоположную от M сторону.

Параллелограмм: внутренняя часть плоскости, ограниченная замкнутой цепочкой из четырех отрезков, в которой противоположные отрезки параллельны друг другу. Граница принадлежит параллелограмму.

У параллелограмма имеются: стороны (граничные отрезки), вершины (точки соединения сторон), углы (внутренние при вершинах), диагонали (отрезки, соединяющие противоположные вершины).

Свойства параллелограмма:

Центром симметрии является точка пересечения диагоналей.

Длины противоположных сторон одинаковы.

Противоположные углы равны между собой.