<< Назад  |   Оглавление  |   Далее >>

4.9. Площади треугольника, параллелограмма, трапеции

Многоугольники

Пусть на плоскости задано n произвольных точек. И пусть они соединены отрезками таким образом, что эти отрезки образуют замкнутую цепочку.

 

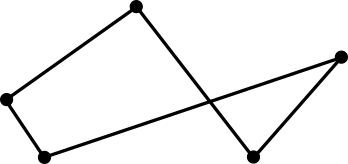
Особенно нас интересует случай, когда цепочка не содержит точек самопересечений и ни одна из пар соседних отрезков не лежит на одной прямой.

 

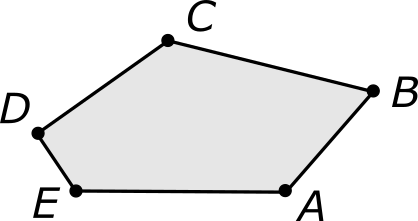
Внутренняя часть плоскости, ограниченная такой цепочкой (включая саму цепочку), называется многоугольником, или, точнее, n-угольником. Многоугольник обычно обозначают перечисляя его вершины. Например, многоугольник, изображенный на рисунке можно обозначить как ABCDE. Мы уже имели дело с одной разновидностью многоугольников, а именно — с параллелограммом [4.4] (и, в частности, с прямоугольником [4.8]). Поэтому нижеследующая терминология должна быть нам уже хорошо знакома.

Отрезки, служащие границей многоугольника называются его сторонами.

Концы сторон, где они соединяются друг с другом, называются вершинами многоугольника.

Внутренние углы между соседними сторонами (при вершинах) называются углами многоугольника.

Отрезки, соединяющие не соседние вершины многоугольника, называются диагоналями.

В ближайшем будущем мы будем рассматривать только такие n-угольники, у которых n равно трем или четырем. Они называются, соответственно, треугольниками и четырехугольниками.

Площадь геометрической фигуры

Как ни странно, такое распространенное понятие, как геометрическая фигура, не имеет общепринятого четкого математического определения. Давайте договоримся, что под (плоской) фигурой мы будем понимать нечто такое, что можно начертить на листе бумаги и вырезать ножницами в виде единого куска. В частности, типичными геометрическими фигурами являются многоугольники. Всякая фигура характеризуется площадью S, которую мы определим таким образом, чтобы выполнялось соотношение

m = ρ∙S,

где m — это масса вырезанной фигуры, а ρ — поверхностная плотность бумаги. Разумеется, мы говорим о бумаге только ради определенности. С тем же успехом можно брать любой другой листовой материал. Поверхностную плотность ρ легко установить, если вырезать из того же материала прямоугольник со сторонами a₀ и b₀ и измерить его массу m₀. Тогда, как мы знаем,

ρ =	m0	.
	a0b0

В случае прямоугольника справедливость соотношения m₀ = ρ∙S₀, где площадь S₀ равна S₀ = a₀b₀, была уже установлена нами ранее.

Разрежем фигуру площадью S и массой m на две части. Тогда массы частей m₁ и m₂ составляют в сумме исходную массу m:

m₁ + m₂ = m.

Поделив обе части этого равенства на ρ, получаем, что площади отдельных частей S₁ и S₂ подчиняются подобному же соотношению:

S₁ + S₂ = S.

Это равенство послужит нам основой для вычисления площади треугольников, да и вообще любых других геометрических фигур.

Площадь прямоугольного треугольника

Треугольник, в котором один из углов — прямой (то есть равен 90°), называется прямоугольным. При этом стороны, примыкающие к прямому углу называются катетами, а сторона, лежащая напротив прямого угла, — гипотенузой. На чертежах прямой угол часто помечается небольшим квадратиком («носиком»), как показано на рисунке.

 

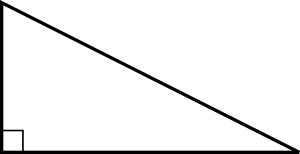
Пусть в треугольнике ABC угол при вершине C равен 90°. Проведем через вершины A и B прямые, параллельные противоположным катетам BC и AC. В результате образуется прямоугольник, выделенный на рисунке серым цветом.

 

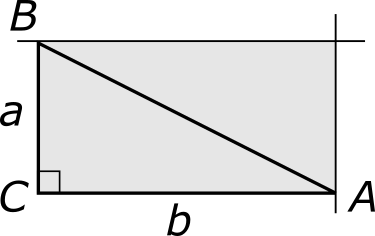
Гипотенуза AB служит прямоугольнику диагональю, причем ее центр является центром симметрии прямоугольника [4.4]. Эта диагональ делит прямоугольник на два симметричных треугольника с одинаковыми площадями S. Взятые вместе, эти площади составляют площадь всего прямоугольника, которая, таким образом, равна 2S. Обозначим длины катетов исходного треугольника через a и b. В прямоугольнике эти катеты играют роль сторон. Следовательно, площадь прямоугольника можно найти как 2S = ab. Отсюда, площадь каждого из треугольников — в том числе, исходного треугольника ABC — равна

Площадь произвольного треугольника

Рассмотрим произвольный треугольник АВС. Выберем одну из его сторон и назовем ее основанием. Пусть для определенности это будет сторона ВС. Обозначим ее длину через a, так что a = |BC|.

 

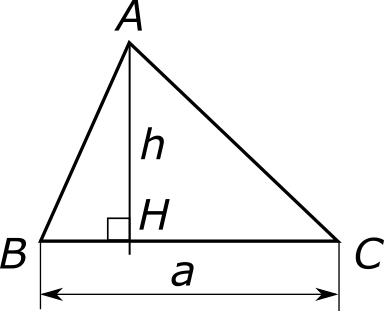
Из противоположной вершины A опустим перпендикуляр на прямую BC и обозначим точку его пересечения с этой прямой через H. Отрезок AH называется высотой треугольника АВС, проведенной к основанию BC. Обозначим длину этого отрезка через h: h = |AH|. Возможны два случая.

Случай 1. Точка H лежит на основании BC.

 

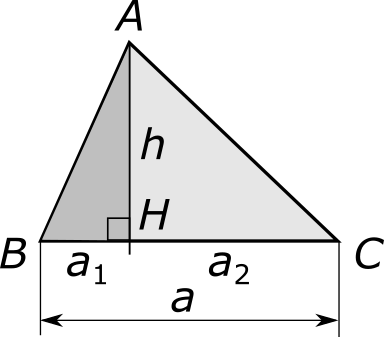
Ведем обозначения: a₁ = |BH| и a₂ = |HC|. Заметим, что a₁ + a₂ = a. Площадь S треугольника ABC найдем как сумму двух прямоугольных треугольников: темно-серого ABH и светло-серого AHC:

S = ½ a₁h + ½ a₂h = ½ (a₁ + a₂) h = ½ ah.

Случай 2. Точка H не принадлежит основанию BC. Пусть, для определенности, она лежит на прямой BC со стороны точки B.

 

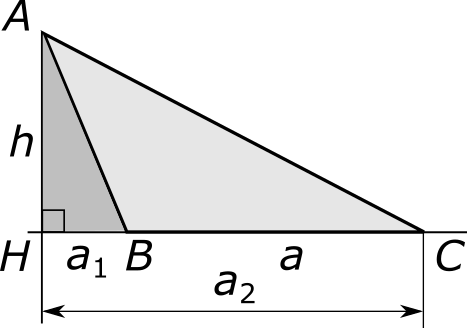
Введем, как и раньше, обозначения a₁ = |BH| и a₂ = |HC|. Длина основания на этот раз равна a = a₂ − a₁. Площадь светло-серого треугольника ABC находим как разность площадей большого «объединенного» треугольника AHC и темно-серого треугольника AHB:

S = ½ a₂h − ½ a₁h = ½ (a₂ − a₁) h = ½ ah.

Таким образом, в обоих случаях мы получили для площади треугольника одну и ту же формулу:

Впрочем, оба случая можно объединить в один, если вспомнить, что мы умеем пользоваться отрицательными числами. Будем считать, что прямая, на которой лежит основание треугольника, представляет собой числовую ось x с нулем в точке H. Положение точек B и C на этой оси обозначим через x_B и x_C. Направление оси выберем так, чтобы выполнялось неравенство x_B < x_C. Далеко в отрицательной области отметим на оси некоторую точку H₁. Через точку A проведем прямую, параллельную оси x, а через точку H₁ — прямую, параллельную высоте AH треугольника ABC. Обозначим пересечение этих прямых через A₁.

 

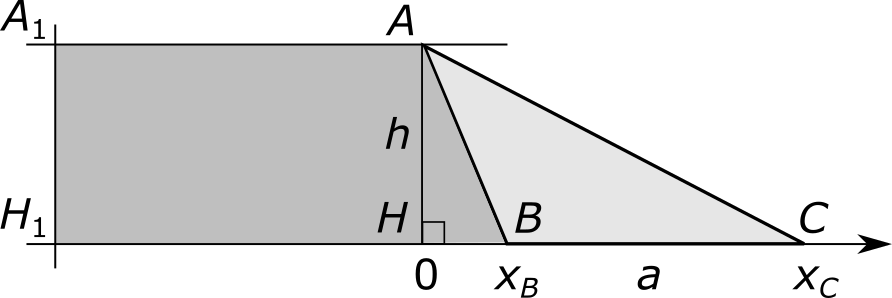
Мы получили прямоугольник AA₁H₁H, площадь которого мы обозначим через S₀. При этом площадь четырехугольника AA₁H₁С равна, очевидно, S₀ + ½ x_Сh. Но нас на самом деле интересует не вся эта площадь целиком, а только ее отклонение от величины S₀. Это отклонение мы для краткости будем называть площадью треугольника AHC. Эта площадь, равная ½ x_Сh, может быть положительной или отрицательной в зависимости от знака числа x_С. Площадь S треугольника ABC может быть вычислена как разность площадей четырехугольников AA₁H₁С и AA₁H₁B:

S = (S₀ + ½ x_Сh) − (S₀ + ½ x_Bh),

или, говоря короче, как разность площадей треугольников AHС и AHB:

S = ½ x_Сh − ½ x_Bh = ½(x_С − x_B)h = ½ ah.

Как и следовало ожидать, результат получился таким же, как раньше.

Расстояние между параллельными прямыми

Рассмотрим две произвольные параллельные прямые m и n. Отметим на прямой m какую-либо точку M и опустим из нее перпендикуляр на прямую n. Обозначим точку пересечения перпендикуляра с прямой n через N.

 

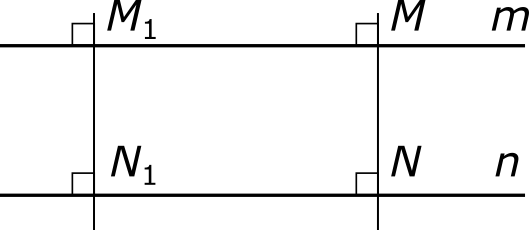
Длина отрезка MN называется расстоянием между прямыми m и n. Это расстояние не зависит от положения точки M на прямой m. Действительно, возьмем на прямой m любую другую точку M₁, проведем через нее перпендикуляр к прямой n, и обозначим новую точку пересечения через N₁. У нас образовался прямоугольник NMM₁N₁, в котором отрезки MN и M₁N₁ являются противоположными сторонами, а потому их длины равны между собой.

Нетрудно также видеть, что точно такое же расстояние между прямыми мы получим, если будем измерять его не от прямой m к прямой n, а наоборот, от прямой n к прямой m.

Площадь трапеции

Трапеция — это четырехугольник, у которого какие-либо две противоположные стороны являются параллельными. Эти параллельные стороны называются основаниями трапеции, а две другие — боковыми сторонами. Расстояние между прямыми, на которых лежат основания, носит название высоты трапеции.

 

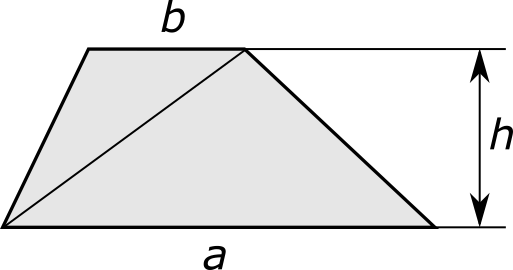
Вычислим площадь S произвольной трапеции. Пусть a и b — длины ее оснований, а h — высота. Проведя в трапеции какую-либо диагональ, разобьем ее таким образом на два треугольника. Площади этих треугольников равны ½ ah и ½ bh, а значит площадь всей трапеции вычисляется как

Площадь параллелограмма

Параллелограмм можно рассматривать как частный случай трапеции. Поскольку, однако, в параллелограмме имеется две пары параллельных сторон, то перед вычислением площади мы должны определиться с тем, чтó именно считать основаниями, а что — боковыми сторонами.

 

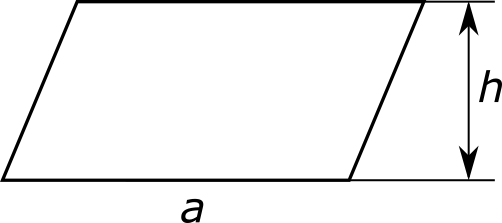
Также следует иметь в виду, что основания в параллелограмме имеют одинаковые длины, которые, таким образом, можно обозначить одной и той же буквой a. Высота h должна соответствовать выбранной паре оснований. С учетом этих оговорок, площадь S параллелограмма можно найти по формуле для площади трапеции, которая преобразуется в

Конспект

1. Многоугольник, n-угольник: часть плоскости внутри ограниченной замкнутой несамопересекающейся цепочки из n отрезков, в которой соседние отрезки не лежат на одной прямой. Граница принадлежит многоугольнику.

2. Площадь S произвольной геометрической фигуры, которую можно вырезать из бумаги, определяется таким образом, чтобы масса m фигуры была равна m = ρ∙S, где ρ — поверхностная плотность бумаги.

3. Площадь прямоугольного треугольника равна половине произведения катетов.

4. Площадь произвольного треугольника равна половине произведения основания на высоту, проведенную к этому основанию.

5. Площадь трапеции равна полусумме оснований, умноженной на высоту.

6. Площадь параллелограмма равна произведению основания на высоту.