<< Назад  |   Оглавление  |   Далее >>

4.7. Графическое решение задач на пропорции. Шкалы

Рассмотрим такую задачу.

Задача 4.7.1. Два метра проволоки весят 10 г. Сколько весят пять метров такой проволоки?

Решение. Первый способ

Нарисуем проволоку, о которой идет речь в условии, и отметим с помощью засечек различные расстояния от ее левого конца.

 

Чтобы рисунок поместился у нас на бумаге, мы изобразили его в уменьшенном масштабе. При этом, однако, числа возле засечек соответствуют немасштабированным длинам — тем, которые были бы измерены вдоль проволоки, а не тем, которые получились у нас на рисунке.

Мы специально поместили засечки только снизу от проволоки, потому что сверху мы сейчас нарисуем засечки другого рода. Каждая такая верхняя засечка будет указывать нам на вес (а точнее — массу) той части проволоки, которая расположена слева от нее. Из условия задачи мы знаем, что верхняя засечка, соответствующая 10 г, должна находиться в том же самом месте, что и нижняя засечка, соответствующая 2 м:

 

Зная местоположение десятиграммовой засечки, мы можем теперь легко расставить засечки для других значений массы:

 

Мы видим, что напротив отметки 5 м находится отметка 25 г. Значит, 5 м проволоки весят 25 г. Задача решена.

Конечно, мы решили задачу не самым простым способом, но зато наш способ нагляден и допускает кое-какие полезные обобщения. Если нас, например, спросят, какова масса трех метров проволоки, то мы, едва взглянув на рисунок, сразу же дадим ответ.

Отметим, что ряд засечек вдоль какой-либо линии с расставленными возле (некоторых из) них числами называют шкалой. Для шкал характерно, что засечки и числа отображают вовсе не фактическую длину линии, вдоль которой они расставлены, а какие-то другие величины. Засечки называют также отметками и — особенно часто — делениями. На нашем рисунке имеется две шкалы. Снизу от прямой находится шкала длин, а сверху — шкала масс. Шкалы позволяют нам, разглядывая сравнительно короткие отрезки на небольшом по размеру рисунке, воображать при этом, что мы имеем дело с гораздо большими расстояниями или даже с величинами, которые к расстоянию не имеют непосредственного отношения, — такими, как масса. Если фактические расстояния вдоль линии пропорциональны отображаемым величинам, то шкала называется пропорциональной или линейной. Мы первое время будем пользоваться только пропорциональными шкалами. Деления в пропорциональных шкалах наносятся обычно через равные промежутки. В этом случае шкалы называют также равномерными.

Второй способ

Вернемся теперь к нашему графическому решению задачи про проволоку. Всем-то оно хорошо, да только годится оно лишь для одного-единственного типа проволоки. Если речь зайдет о проволоке другого диаметра или из другого материала, то нам придется перечерчивать весь рисунок. Давайте попробуем придумать более общее решение.

Поскольку на нашем рисунке вдоль одной и той же линии расположены две разные шкалы, мы легко можем себе представить, что это не одна линия, а две — просто они совпадают друг с другом. Повернем линию с верхней шкалой на некоторое угловое расстояние вокруг левого конца проволоки. Мы получим угол, на каждую сторону которого приходится по одной шкале.

 

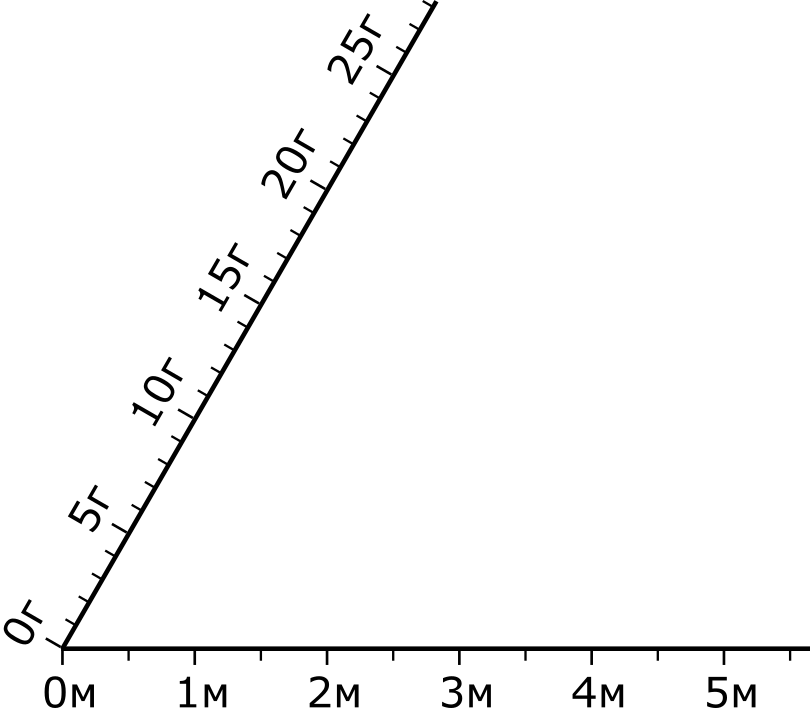
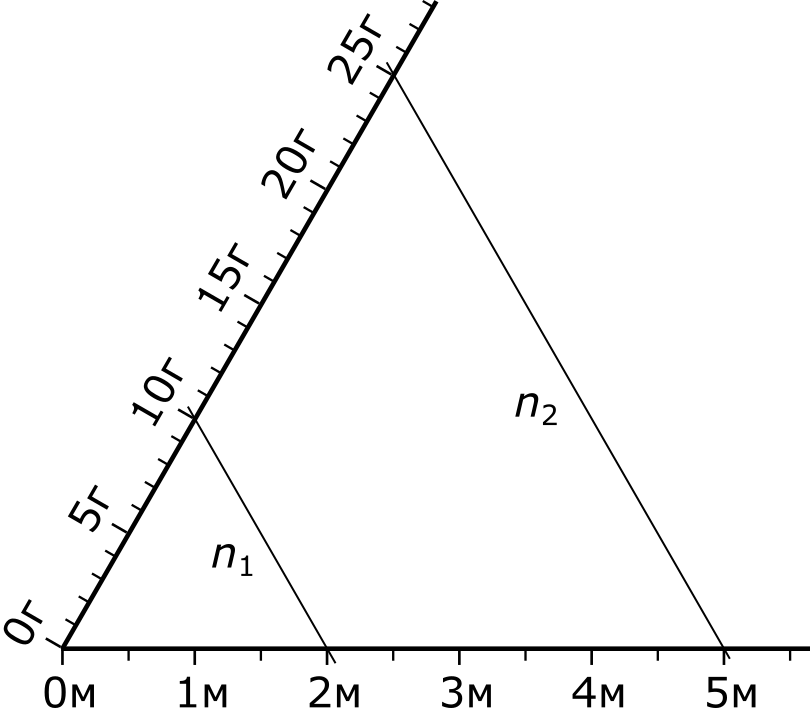
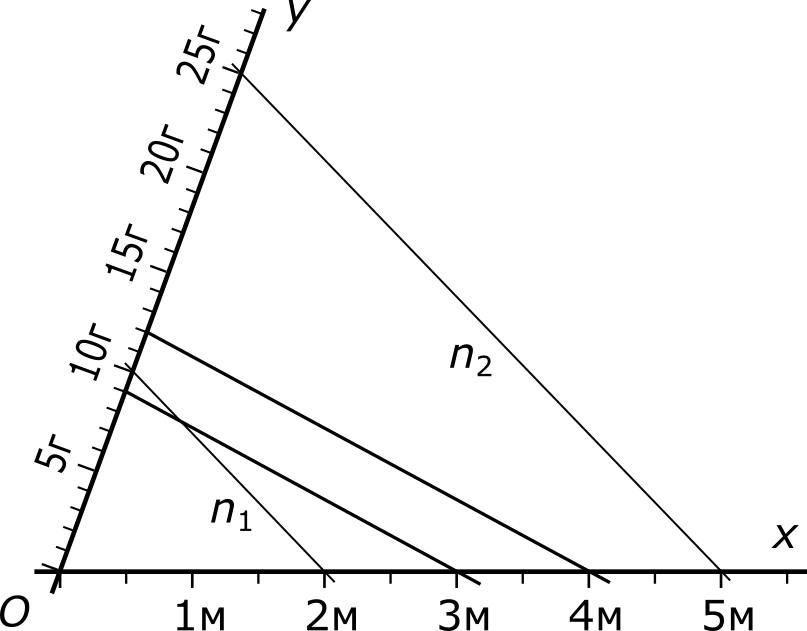
Согласно условию, два метра проволоки весят десять грамм. Соединим поэтому отметки 2 м и 10 г прямой n₁. Чтобы определить массу пяти метров проволоки, проведем через отметку 5 м прямую n₂, параллельную прямой n₁. Эта прямая отсечет на шкале масс искомый ответ.

 

Поскольку наше второе решение исторически опирается на первое, то наш рисунок устроен так, что фактическая длина отрезка, соответствующего двум метрам на одной шкале, в точности совпадает с фактической длиной отрезка, соответствующего десяти граммам на другой шкале. Но в действительности этого совершенно не нужно. Перечертим наш рисунок еще раз. Вначале построим две прямые x и y, пересекающиеся в некоторой точке O под произвольным углом α (0 ≠ α ≠ 180°). Затем нанесем на прямую x шкалу длин, а на прямую y — совершенно независимую шкалу масс, так чтобы обе шкалы начинались в точке O.

 

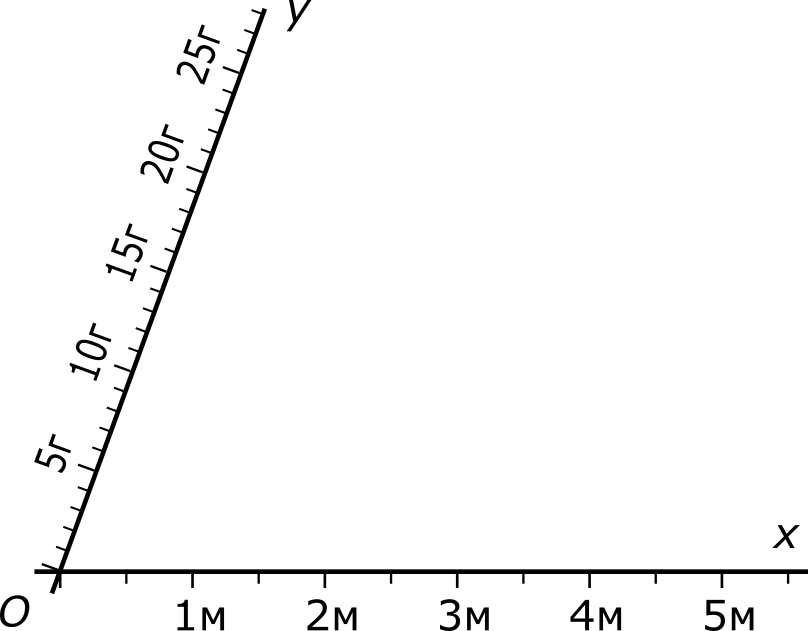
Соединим отметки 2 м и 10 г прямой n₁. Параллельно ей проведем через отметку 5 м прямую n₂. После этого остается только посмотреть на точку пересечения прямой n₂ со шкалой масс и — сказать ответ.

 

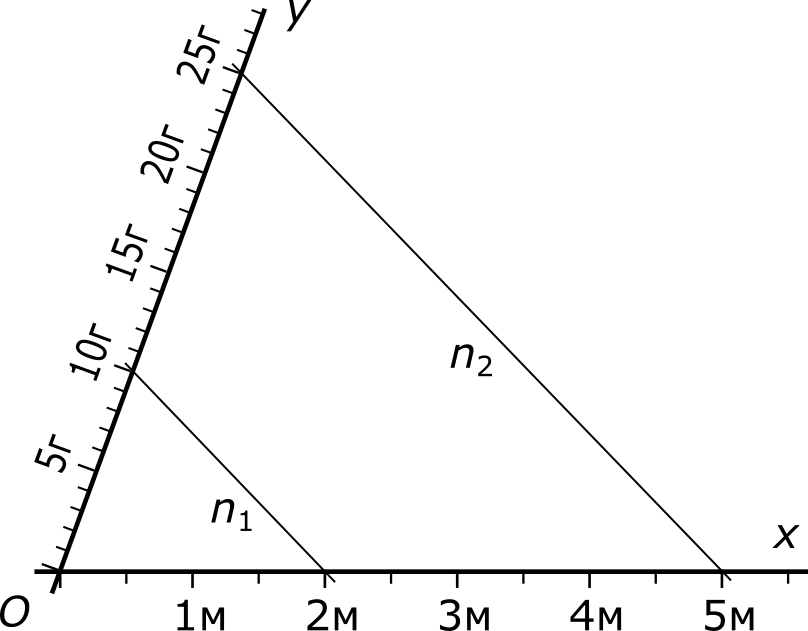
Теперь мы может решать задачи про другие типы проволок, не перечерчивая наших шкал. Пусть, например, нам скажут, что моток длиной три метра весит 9 г и попросят вычислить массу двенадцати метров такой проволоки. Мы проводим на нашем рисунке еще две параллельные прямые — и ответ готов.

 

Третий способ (самый популярный)

Задачу про проволоку можно решить еще одним способом, который, впрочем, очень похож на предыдущий. Шкалы длин и масс рисуются на пересекающихся осях x и y точно так же, как и в прошлый раз:

 

Дальнейшие построения проведем для проволоки, два метра которой весят 10 г:

Через отметку 2 м на оси x проведем прямую y₁, параллельную оси y, а через отметку 10 г на оси y — прямую x₁, параллельную оси x.

Точку пересечения прямых x₁ и y₁ обозначим через P₁ и проведем прямую p через точки O и P₁.

 

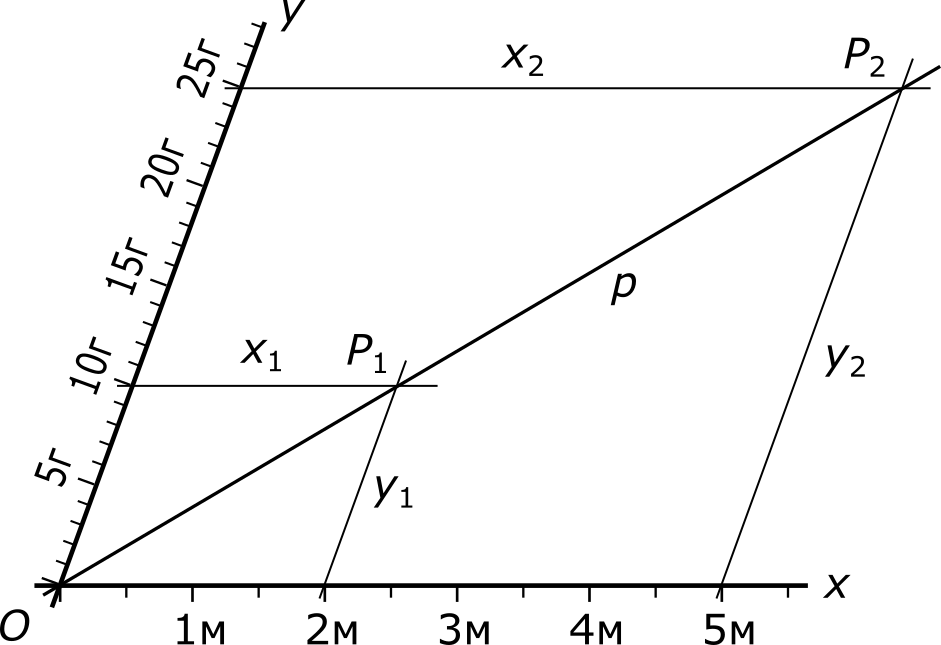
Допустим, мы теперь хотим узнать, сколько весят 5 м проволоки.

Через отметку 5 м на оси х проводим прямую у₂, параллельную оси у. Она пересекает прямую p в некоторой точке P₂.

Через точку P₂ проводим прямую x₂, параллельную оси x. Она отсекает на оси y искомый ответ.

Это решение хорошо тем, что чертеж очень удобно рисовать на листе бумаги в клеточку, какие обычно используются в школе для занятий по математике. При этом угол α между осями x и y берут равным 90°. В этом случае оказывается, что большинство линий, необходимых для построения, совпадает с линовкой бумаги.

 

Негеометрический способ

Геометрические построения очень полезны для понимания сути задачи, однако они не являются обязательными. Старый добрый способ решения задач на подобие заключается в том, чтобы поначалу составить что-то вроде таблички:

2 м  —  10 г
5 м  —    y

Вместо неизвестной нам пока массы пяти метров проволоки мы написали здесь переменную y. Эта табличка читается примерно так:

Длина 2 метра соответствует массе 10 грамм.
Длина 5 метров соответствует массе y.

Теперь, глядя на табличку, рассуждаем так. При увеличении длины проволоки в k раз ее масса также увеличивается в k раз. В данном случае k = 5 м / 2 м. А значит, мы можем написать пропорцию:

y	=	5 м	.
10 г		2 м

Эта пропорция представляет собой не что иное, как уравнение относительно неизвестной переменной y. Решая его, находим:

y =	10 г ∙ 5 м	= 25 г.
	2 м

Таким образом, мы опять пришли к тому, что пять метров проволоки весят 25 г.

Для тех, кто хорошенько поднаторел в решении задач на пропорции, вовсе не обязательно проводить всякий раз одни и те же рассуждения. Можно просто, взглянув на табличку, сразу написать ответ. Мысленно проведем в табличке диагонали:

 

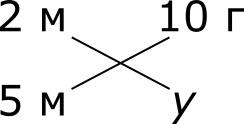
Тогда неизвестная величина y находится по следующему правилу:

y =	произведение чисел, находящихся на «чужой» диагонали	.
	число, расположенное на другом конце «своей» диагонали

В данном случае, числа, находящиеся на «чужой» диагонали — это 10 г и 5 м. Число, расположенное на другом конце «своей» диагонали — это 2 м.

Вообще говоря, при решении задач на пропорции неизвестная величина может оказаться в произвольном месте таблички. Однако правило сформулировано так, что оно остается справедливым в любом случае.

Линейная плотность

Решим теперь задачу про проволоку в общем виде. Пусть известно, что проволока длиной L₀ имеет массу m₀. Требуется найти массу m проволоки длиной L. Табличка в этом случае выглядит так:

L₀  —  m₀
L    —  m

Отсюда

m =	m0	∙ L.
	L0

Мы получили формулу зависимости массы проволоки m от ее длины L. Эта формула верна, разумеется, при любом значении L₀. В качестве L₀ мы могли бы с одинаковым успехом взять и 1 см, и 1 м, и 10 м. Какую бы длину L₀ мы ни взяли, отношение m₀/L₀ будет всегда равно одному и тому же числу (имеющему размерность г/м). Это число характеризует данный тип проволоки и не зависит от ее длины. Оно называется линейной плотностью и нередко обозначается греческой буквой ρ:

ρ =	m0	=	m	.
	L0		L

Таким образом, чтобы найти массу m проволоки, надо умножить ее линейную плотность ρ на длину L:

m = ρL.

Линейная зависимость

Если переменные x и y связаны между собой соотношением

y = k ∙ x,

где k — некоторое постоянное число, то говорят, что

переменная y (прямо) пропорциональна переменной x

или

переменная y линейно зависит от переменной x,

при этом число k называется коэффициентом пропорциональности. Например, масса m проволоки прямо пропорциональна ее длине L, а в качестве коэффициента пропроциональности в этом случае выступает линейная плотность ρ.

Конспект

Мы рассмотрели задачу типа: «Проволока длиной L₀ имеет массу m₀. Найти массу m проволоки длиной L». Графическое решение состоит в том, чтобы начертить шкалу длин и шкалу масс и выстроить соответствие между этими двумя шкалами. Это можно сделать (как минимум) тремя способами. «Формульное» решение таково: m = ρL, где ρ = m₀/L₀ — линейная плотность проволоки. Таким образом, m пропорционально L с коэффицентом пропорциональности ρ.