<< Назад  |   Оглавление  |   Далее >>

4.6. Обобщенная теорема Фалеса. Пропорции. Масштаб

Пропорции

Равенство вида

x1	=	y1
x2		y2

называется пропорцией. При этом говорят, что:

x₁ относится к x₂ как y₁ относится к y₂,

или

отношение чисел x₁ и x₂ равно отношению чисел y₁ и y₂,

или же

числа x₁ и x₂ соотносятся так же, как числа y₁ и y₂,

или, наконец,

числа x₁ и y₁ (!) пропорциональны числам x₂ и y₂ (то есть числители пропорциональны знаменателям).

Входящие сюда числа x₁, x₂, y₁ и y₂ называются членами пропорции. Обычно все они положительны, но это необязательно. Предполагается, однако, что ни одно из них не равно нулю. Особого названия это равенство удостоилось по той причине, что оно часто встречается при решении разных математических задач.

 

Пропорции можно преобразовывать, перенося члены «с верху» одной части равенства «в низ» другой части равенства и наоборот. Эту процедуру легко обосновать следующим образом. Допустим мы хотим перенести x₁ из левой части в правую. Для этого умножим обе части пропорции на 1/x₁:

1		x1	=	1		y1	.
x1		x2		x1		y2

В результате получаем

1	=	y1	,
x2		x1y2

то есть переменная x₁ у нас переместилась «по диагонали сверху вниз». Перенесем теперь «влево наверх» переменную y₂. Это достигается умножением на нее обеих частей данного равенства. В результате имеем

y2	=	y1	.
x2		x1

Мы получили новую пропорцию, которая отличается от исходной перестановкой членов, расположенных «по диагонали». Таким образом, в первоначальном равенстве

x1	=	y1
x2		y2

числители x₁ и y₁ соотносятся между собой точно так же, как и соответствующие им знаменатели x₂ и y₂.

Обобщенная теорема Фалеса

Теорема Фалеса, рассмотренная в прошлый раз, допускает следующее обобщение.

Пусть две произвольные прямые x и y пересекаются тремя параллельными прямыми n₁, n₂ и n₃ в точках X₁, X₂, X₃ и Y₁, Y₂, Y₃, как показано на рисунке:

 

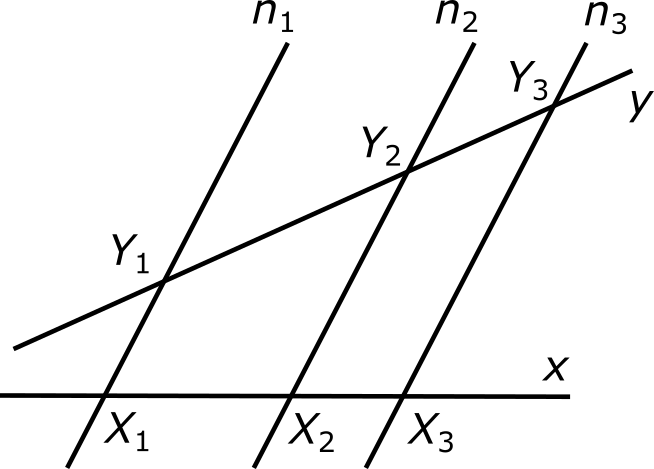
Тогда длины отсекаемых отрезков образуют следующую пропорцию

|Y1Y2|	=	|X1X2|	.
|Y1Y3|		|X1X3|

Докажем эту теорему в случае, когда отношение длин

|X1X2|

|X1X3|

представляет собой рациональное число, то есть может быть выражено в виде несократимой дроби

|X1X2|	=	a	,
|X1X3|		b

где a и b — некоторые натуральные числа, a < b. Разобьем отрезок X₁X₃ на b одинаковых частей. (При этом точка X₂ окажется одной из точек деления.) Проведем через каждую точку деления прямые, параллельные n₁, n₂ и n₃. (Одна из этих прямых совпадет с прямой n₂.)

 

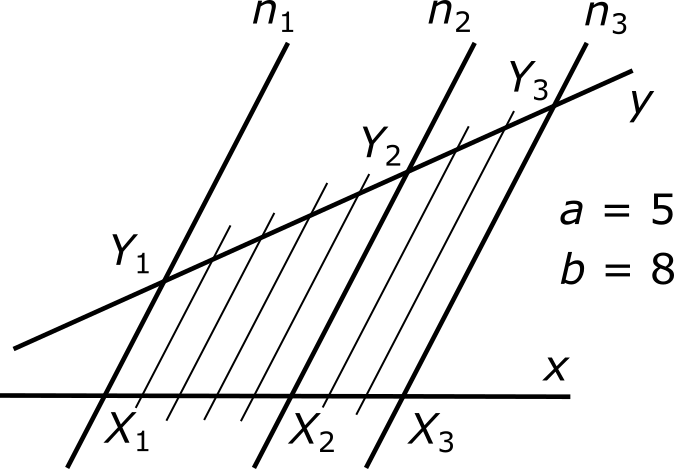
По теореме Фалеса (в ее первоначальном варианте), отрезок Y₁Y₃ также делится этими прямыми на b равных частей, из которых a частей составляют отрезок Y₁Y₂. Следовательно,

|Y1Y2|	=	a	=	|X1X2|	,
|Y1Y3|		b		|X1X3|

что и требовалось доказать. Из нашего построения следует также, что

|Y2Y3|	=	b − a	=	|X2X3|
|Y1Y3|		b		|X1X3|

и

|Y2Y3|	=	b − a	=	|X2X3|	.
|Y1Y2|		a		|X1X2|

Пользуясь свойствами пропорций, эти равенства можно переписать в виде одной цепочки:

|Y1Y2|	=	|Y2Y3|	=	|Y1Y3|	.
|X1X2|		|X2X3|		|X1X3|

Таким образом, отрезки отсекаемые на прямой y пропорциональны соответствующим отрезкам на прямой x.

 

Теоретически возможна также ситуация, когда отношение длин

|X1X2|

|X1X3|

не является рациональным числом, поскольку длины отрезков |X₁X₂| и |X₁X₃| могут, в принципе, выражаться иррациональными числами. Однако на практике такой случай никогда не встречается. Для определения длин отрезков мы всегда пользуемся каким-либо измерительным прибором (например, школьной линейкой), который выдает лишь округленные результаты в виде конечной десятичной дроби.

Важное следствие

Пусть даны несовпадающие прямые x и y, которые пересекаются в точке O, и еще — две параллельные прямые n₁ и n₂, которые пересекают прямую x в точках X₁ и X₂ и прямую y в точках Y₁ и Y₂, как показано на рисунке.

 

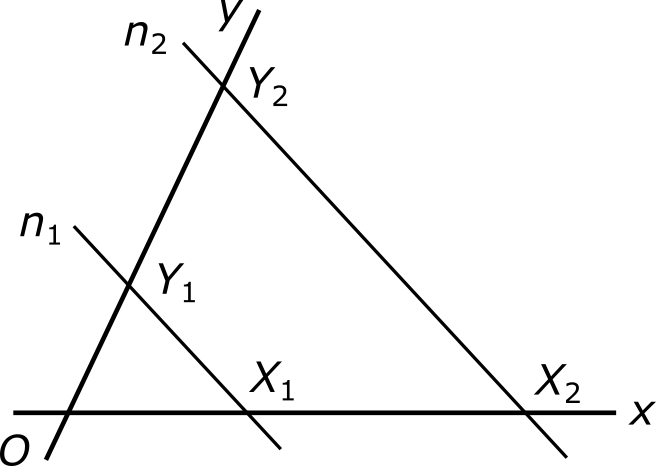
Введем обозначения:

x₁ = |OX₁|, x₂ = |OX₂|;

y₁ = |OY₁|, y₂ = |OY₂|;

z₁ = |X₁Y₁|, z₂ = |X₂Y₂|.

Тогда

x1	=	y1	=	z1	.
x2		y2		z2

Действительно, оба равенства в этой цепочке непосредственно следует из обобщенной теоремы Фалеса. Для первого равенства это ясно сразу, а для второго это становится очевидным после того, как мы через точку Y₁ проведем прямую m, параллельную прямой x.

 

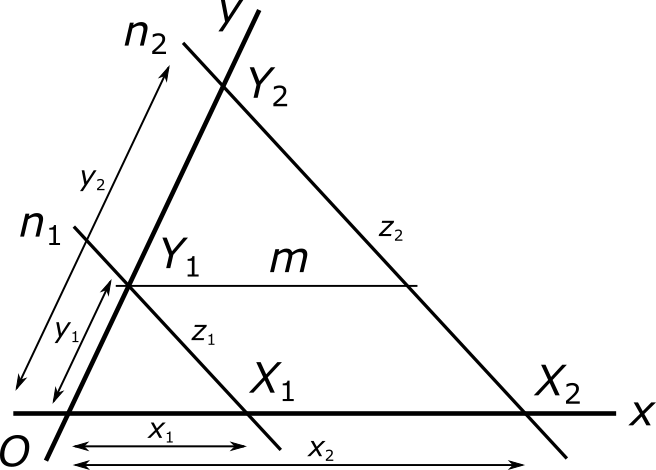
Верно и обратное утверждение. Пусть дана та же геометрическая конструкция и известно, что

x1	=	y1	.
x2		y2

Тогда прямые n₁ и n₂ параллельны. В самом деле, проведем через точку X₁ вспомогательную прямую, параллельную прямой n₂. По обобщенной теореме Фалеса, эта вспомогательная прямая проходит через точку Y₁. Следовательно, она совпадает с прямой n₁. Таким образом, прямая n₁ параллельна прямой n₂.

Масштаб

Выйдем на улицу, прихватив с собой лист бумаги и карандаш. Расположим наш лист горизонтально и поставим на нем приблизительно посередине точку O. Из этой точки проведем мысленно лучи в направлении различных примечательных точек на местности, расположенных в радиусе примерно ста метров, — деревьев, столбов, углов зданий и того подобного.

Допустим, у нас есть возможность измерить расстояния до этих примечательных точек. Пусть, например, расстояние до ближайшего дерева равно 10 м. Мысленно отложим от точки O в направлении этого дерева отрезок, длина которого в 1000 раз меньше данного расстояния, и отметим карандашом на бумаге положение второго его конца. Нетрудно рассчитать, что расстояние от точки O до отметки составит 10 м/1000 = 1 см.

Подобным же образом, пусть расстояние до какого-то другого примечательного объекта равно x₁. Умножим это расстояние на число k, равное 1/1000. Мысленно отложим от точки O отрезок длиной x₂ = kx₁ вдоль луча, направленного на данный объект. В том месте на бумаге, где находится второй конец отрезка, сделаем отметку карандашом. Проделаем такую процедуру со всеми примечательными точками на местности, используя всё время одно и то же значение параметра k. Если какие-либо из этих точек соединены между собой забором или стеной или же чем-то подобным, то между соответствующими метками на бумаге также проведем линии.

В результате на нашем листе бумаги получится карта местности. В силу теоремы Фалеса и свойств пропорций, все соотношения между расстояниями на бумаге будут в точности такими же, как и в действительности. Более того, все линии на бумаге окажутся параллельны соответствующим линиям на местности. Эта параллельность, конечно, нарушится, когда мы унесем наш лист куда-нибудь в другое место, однако углы между линиями сохранятся.

Параметр k, который мы использовали в нашем построении, называется масштабным коэффициентом или просто масштабом. Разумеется, он необязательно должен быть равен 1/1000. Он может, в принципе, принимать любое значение, важно лишь, чтобы это значение оставалось всё время неизменным в процессе построения карты.

На настоящих географических картах масштаб обязательно указывается в легенде, при этом вместо дробной черты обычно используется двоеточие. Например, масштаб 1:100 000 означает, что один сантиметр на карте соответствует 100000 сантиметрам (то есть одному километру) на местности.

Технические чертежи также всегда выполняются, как говорят,  в определенном масштабе. Масштаб 1:1 означает, что деталь начерчена в натуральную величину. А масштаб 10:1 говорит о том, что чертеж выполнен с десятикратным увеличением.

Замечание о параллельных прямых

Мы назвали параллельными такие несовпадающие прямые, угол между которыми равен нулю. Мы отметили, что такие прямые нигде не пересекаются. Докажем теперь, что если прямые лежат в одной плоскости и не параллельны (то есть угол между ними отличен от нуля), то тогда они обязательно где-нибудь пересекутся.

Пусть на плоскости даны две прямые — x и n. Отметим на них произвольные точки — O и Y — и проведем через эти точки третью прямую — y. Если исходить из того, что угол между прямыми x и n не равен нулю, то смежные углы должны оказаться не равны друг другу. Пусть для определенности α₁ > α₂, как показано на рисунке.

 

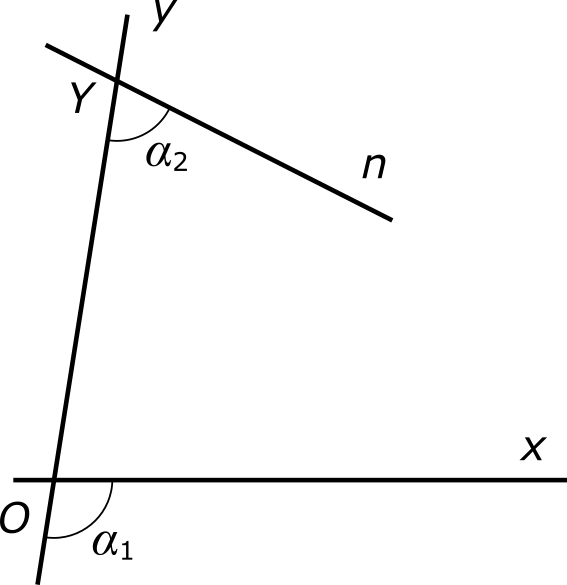
Проведем через точку O прямую n₁, параллельную прямой n. Отметим на ней со стороны угла α₁ произвольную точку N₁ и проведем через эту точку прямую y₁, параллельную прямой y. При этом образуется параллелограмм, обозначенный на рисунке серым фоном.

 

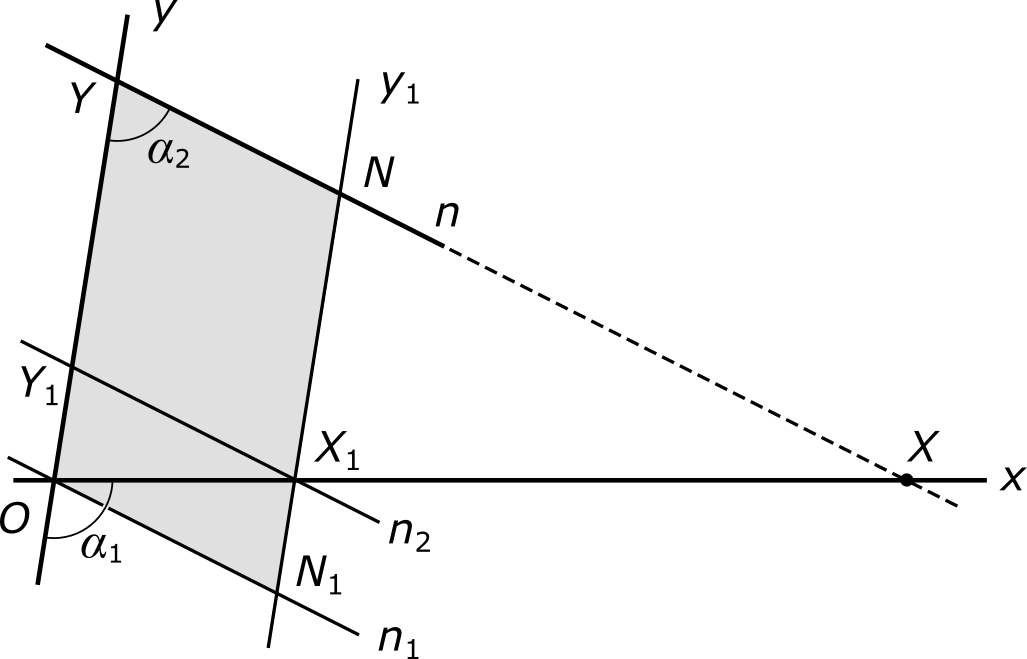
Это значит, что прямая y₁ пересекает прямую n в некоторой точке, которую мы обозначим через N. Прямая x, заходя на «территорию» параллелограмма в точке O, обязательно должна где-то оттуда выйти. Она может это сделать либо через отрезок YN, либо через отрезок N₁N. В первом случае сразу становится очевидно, что прямая x пересекает прямую n. Рассмотрим второй случай. Обозначим точку пересечения прямой x и отрезка N₁N через X₁. Проведем через нее прямую n₂, параллельную прямой n. Эта прямая разбивает параллелограмм ON₁NY на два новых параллелограмма и пересекает прямую y в некоторой точке Y₁. Отметим на прямой x такую точку X, для которой выполняется соотношение

|OY1|	=	|OX1|	.
|OY|		|OX|

Проведем через точки X и Y прямую. Согласно рассмотренному выше следствию из теоремы Фалеса, эта прямая параллельна прямой n₂, а значит, образует нулевой угол с прямой n. Следовательно, новая прямая совпадает с прямой n, которая, таким образом, пересекает прямую x в точке X.

Мы теперь можем утверждать, что следующие три утверждения о несовпадающих прямых a и b, лежащих в одной плоскости, означают в точности одно и то же:

(1) Угол между прямыми a и b равен нулю.

(2) Прямые a и b нигде не пересекаются.

(3) Прямые a и b параллельны.

В традиционных курсах геометрии определением параллельности прямых служит утверждение 2. Мы выбрали для этих целей утверждение 1. Ведь гораздо проще определить угол между двумя прямыми, чем удостовериться, что они нигде не пересекаются на всём своем бесконечном протяжении.

Конспект

1. Равенство вида x₁/x₂ = y₁/y₂ называется пропорцией. Числители пропорциональны знаменателям. Числитель и знаменатель одной дроби соотносятся так же, как числитель и знаменатель другой дроби. Эквивалентное равенство: x₁/y₁ = x₂/y₂.

2. Обобщенная теорема Фалеса. Пусть две произвольные прямые a и b пересекаются тремя параллельными прямыми. Тогда отрезки, отсекаемые на прямой a, пропорциональны соответствующим отрезкам, отсекаемым на прямой b.

3. Следствие 1. Пусть стороны угла с вершиной в точке O пересекаются двумя параллельными прямыми n₁ и n₂. Тогда отрезки, отсекаемые на прямых n₁ и n₂, соотносятся так же, как отрезки, отложенные на любой из сторон угла от точки O до соответствующих точек пересечения с прямыми n₁ и n₂.

4. Следствие 2. Пусть на сторонах угла отложены от вершины отрезки таким образом, что отрезки на одной стороне пропорциональны отрезкам на другой. Тогда прямые, проходящие через соответствующие концы этих отрезков, параллельны друг другу.

5. На карте сохраняются все соотношения между расстояниями и все углы. Отношение расстояния между некоторыми двумя точками на карте к расстоянию между соответствующими точками на местности не зависит от выбора точек и называется масштабом.

6. Если угол между двумя прямыми, лежащими в одной плоскости, не равен нулю, то такие прямые обязательно пересекаются.